11311. Distance to special point
This is an interactive problem
On the plane the integer points with
coordinates does not exceeding 106 are labeled. The movement is
allowed along the lines that are parallel to the coordinate axis, so the
distance between two points that have coordinates x1, y1 and x2, y2 is calculated as |x1 – x2| + |y1 – y2|.
There is unknown special labeled point A.
You may for one query ask the distance from the labeled point you choose to the
point A. Your task is to guess the coordinates of A for two queries.
Interaction Protocol
The interaction is started by your program.
You may ask the queries in the format “? x y” – ask the distance (in definitions of the task) from
the labeled point with coordinates x, y to the point A (-106 ≤ x, y ≤ 106, x and y are integers).
If you are ready to print the answer, use
the following format: “! x y” (x
and y are the coordinates of the point A, then exit the program. This
action is not considered as a query.
Note
For the correct interaction print the
end-of-line after each query and after the answer and flush the output buffer
with the respective functions of your programming language:
·
cout.flush()
or fflush(stdout) for C/C++;
·
stdout.flush()
for Python;
·
look
your language documentation for the other languages.
|
Sample
input |
Sample
output |
|
1 0 |
? 0 0 ? 1 0 ! 1 0 |
SOLUTION
mathematics
Algorithm analysis
Let INF = 106. Let’s make two
queries at points X(-INF, -INF) è Y(INF, -INF).
Let O(x, y) be the
coordinates of unknown point.
Let d(O, X) = a, d(O, Y) = b.
Here d(O, X) denotes the distance between points O and X.
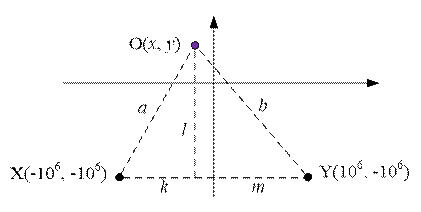
We
have a system: 
, wherefrom a
+ b = k + m + 2l. Considering
that k + m = 2 * INF,
we have: a + b = 2 * INF + 2l. Hence l = (a + b – 2 * INF) / 2.
Knowing
the value of l, we can find the y coordinate
of the unknown point: y = – INF + l.
Since a = k
+ l, then k = a – l.
The abscissa of the unknown point is x = – INF + k = – INF + a
– l.
Thus, the point has coordinates O(– INF + a – l, – INF + l).
Algorithm realization
Define
a constant INF =
106.
#define INF 1000000
The
function ask returns the distance res from the unknown point to
the point (x, y).
int ask(int x, int y)
{
Print
a query – find the distance from the unknown point to (x, y).
printf("? %d %d\n", x, y);
Clean
the output buffer for correct interaction between the program and the
interactor.
fflush(stdout);
int res;
Read
and return the interactor’s response – the distance from the unknown point to (x, y).
scanf("%d", &res);
return res;
}
The main part of the program.
Let’s find the distances a = d(O, X) and b = d(O, Y), where O(x, y) is the unknown point, X(-INF, -INF), Y(INF, -INF).
int a = ask(-INF, -INF);
int b = ask(INF, -INF);
Find
the length of the segment l.
int l = (a + b - 2 * INF) / 2;
Compute
the coordinates (x,
y) of unknown point.
int x = -INF + a - l;
int y = -INF + l;
Print
the coordinates of the unknown point and clear the output buffer.
printf("! %d %d\n", x, y);
fflush(stdout);
Below is the full program.
#include <stdio.h>
#define INF 1000000
int ask(int x, int y)
{
printf("? %d %d\n", x, y);
fflush(stdout);
int res;
scanf("%d",
&res);
return res;
}
int main()
{
int a = ask(-INF, -INF);
int b = ask(INF, -INF);
int l = (a + b - 2 * INF) / 2;
int x = -INF + a - l;
int y = -INF + l;
printf("! %d %d\n", x, y);
fflush(stdout);
return 0;
}